Table of contents
- In this note, $f\in\mathbb{F}^\mathbb{G}$ stands for a function with domain in $\mathbb{G}$ and co-domain in $\mathbb{F}$, i.e. $f:\mathbb{F}\to\mathbb{G}$, $H(x)$ generally stands for Heaviside function (step function)
- Please read the Algebra Basics notes first if you are not familiar with related concepts.
Transforms
Laplace Transform
- Definition: $F(s)=\mathcal{L}\{f(t)\}(s)=\int^\infty_0 f(t)e^{-st}\mathrm{d}t$
Note that the transform is not well defined for all functions in $\mathbb{C}^\mathbb{R}$. And the transform is only valid for $s$ in a region of convergence, which is usually separated by 0.
- Laplace Transform is a linear map from $(\mathbb{C}^\mathbb{R}, \mathbb{C})$ to $(\mathbb{C}^\mathbb{C}, \mathbb{C})$ and it’s one-to-one.
- Properties: (see Wikipedia or this page for full list)
- Derivative: $f’(t) \xleftrightarrow{\mathcal{L}} sF(s)-f(0^-)$
- Integration: $\int^t_0 f(\tau)d\tau \xleftrightarrow{\mathcal{L}} \frac{1}{s}F(s)$
- Delay: $f(t-a)H(t-a) \xleftrightarrow{\mathcal{L}} e^{-as}F(s)$
- Convolution: $\int^t_0 f(\tau)g(t-\tau)\mathrm{d}\tau \xleftrightarrow{\mathcal{L}} F(s)G(s)$
- Stationary Value: $\lim\limits_{t\to 0} f(t) = \lim\limits_{s\to \infty} sF(s), \lim\limits_{t\to \infty} f(t) = \lim\limits_{s\to 0} sF(s)$
Inverse Laplace Transform
Laplace transform is one-to-one, so we can apply inverse transform on functions in s-space
There are several ways to calculate Laplace transform, the first one is directly evaluating integration while the latter two are converting the function into certain formats that are convenient for table lookup:
- (Mellin’s) Inverse formula: $f(t)=\mathcal{L}^{-1}\{F(s)\}(t)=\frac{1}{2\pi j}\lim\limits_{T\to\infty} \int ^{\gamma+iT}_{\gamma-iT} e^{st}F(s)\mathrm{d}s$ where the integration is done along the vertical line $Re(s)=\gamma$ in the convex s-plane such that $\gamma$ is greater than the real part of all poles of $F(s)$.
- Power Series: $F(s) = \sum^\infty_{n=0} \frac{n!a_n}{s^{n+1}}\xleftrightarrow{\mathcal{L}} f(t) = \sum ^\infty_{n=0} a_n t^n $
- Partial Fractions: $F(s)=\frac{k_1}{s+a}+\frac{k_2}{s+b}+\ldots \xleftrightarrow{\mathcal{L}} f(t)=k_1 e^{-at} + k_2 e^{-bt} + \ldots$
- To calculate partial fractions, one can use Polynomial Division or following lemma:
- Suppose $F(s)=\frac{N(s)}{D(s)}=\frac{N(s)}{\prod^n_{i=1} (s-p_i)^{r_i}}$ where $\mathrm{deg}(N(s)) < \mathrm{deg(D(s))}$ and each $p_i$ is a distinct root of $D(s)$ (i.e. pole) with multiplicity $r_i$, then $F(s)=\sum^n_{i=1}\sum^{r_i}_ {j=1} \frac{k_{ij}}{(s-p_i)j}$ where $k_{ij}=\frac{1}{(r_i-j)!}\left.\frac{\mathrm{d}^{r_i-j}}{\mathrm{d}s^{r_i-j}}(s-p_i)^{r_i}F(s)\right\vert_{s=p_i}$
Z-Transfrom
- Definition: $F(z)=\mathcal{Z}\{f(k)_ {k\in\mathbb{N}}\}(z)=\sum^\infty_{k=0} f(k)z^{-k}$
Notice that $f$ is defined on natural numbers. In time domain, it’s usually corresponding to $f(kT)$. Z-transform is also only valid for $z$ in certain region (usually separated by 1)
- Laplace Transform is a linear map from $(\mathbb{C}^\mathbb{N}, \mathbb{C})$ to $(\mathbb{C}^\mathbb{C}, \mathbb{C})$ and it’s one-to-one.
- Properties: (see Wikipedia or this page for full list)
- Accumulation: $\sum^n_{k=-\infty} f(k) \xleftrightarrow{\mathcal{Z}} \frac{1}{1-z^{-1}}F(z)$
- Delay: $f(k-m) \xleftrightarrow{\mathcal{Z}} z^{-m}F(z)$
- Convolution: $\sum^k_{n=0}f_1(n)f_2(k-n) \xleftrightarrow{\mathcal{Z}} F_1(z)F_2(z)$
- Stationary Value: $\lim\limits_{t\to 0} f(t) = \lim\limits_{z\to \infty} F(z), \lim\limits_{t\to \infty} f(t) = \lim\limits_{z\to 1} (z-1)F(z)$
Example: Z-Transform of PID controller
Assume the close-loop error input of the controller is $e(t)$, and $e(kT)$ after sampling. PID controller action in analog is $$m(t)=K\left(e(t)+\frac{1}{T_i}\int^t_0e(t)\mathrm{d}t+T_d\frac{\mathrm{d}e(t)}{\mathrm{d}t}\right)$$ We can approximate by trapezoidal rule with two point difference: $$m(kT)=K\left(e(kT)+\frac{T}{T_i}\sum^k_{h=1}\frac{e((h-1)T)+e(hT)}{2}+T_d\left(\frac{e(kT)-e((k-1)T)}{T}\right)\right)$$ Lets define $f(hT) = \frac{1}{2}\left(e((h-1)T)+e(hT)\right),\;f(0)=0$ Then $$\begin{split}\mathcal{Z}\left(\left\{\sum^k_{h=1}\frac{e((h-1)T)+e(hT)}{2}\right\}_k\right)(z)=\mathcal{Z}\left(\left\{\sum^k_{h=1}f(hT)\right\}_k\right)(z) \\ =\frac{1}{1-z^{-1}}(F(z)-F(0))=\frac{1}{1-z^{-1}}F(z)\end{split}$$ Notice that $$F(z)=\mathcal{Z}\left({f(hT)}_h\right)(z)=\frac{1+z^{-1}}{2}E(z)$$ so we can calculate the Z-transform of $m(kT)$ $$\begin{split} M(z)&=K\left(1+\frac{T}{2T_i}\left(\frac{1+z^{-1}}{1-z^{-1}}\right)+\frac{T_d}{T}(1-z^{-1})\right)E(z)\\&=K\left(1-\frac{T}{2T_i}+\frac{T}{T_i}\frac{1}{1-z^{-1}}+\frac{T_d}{T}(1-z^{-1})\right)E(z)\\&=\left(K_p+K_i\left(\frac{1}{1-z^-1}\right)+K_d(1-z^{-1})\right)E(z) \end{split}$$Here we have
- Proportional Gain $K_p=K-\frac{KT}{2T_i}$
- Integral Gain $K_I=\frac{KT}{T_i}$
- Derivative Gain $K_d=\frac{KT_d}{T}$
Inverse Z-Transform
- Inverse formula: $f(k)=\mathcal{Z}^{-1}\{F(z)\}(k)=\frac{1}{2\pi j}\oint _\Gamma z^{k-1}F(z)\mathrm{d}z$ where the integration is done along any closed path $\Gamma$ that encloses all finite poles of $z^{k-1}X(z)$ in the z-plane.
- According to residual theorem, we can write it as $f(k)=\sum_{p_i}Res(z^{k-1}f(z), pi)$ where $p_i$ are poles of $z^{k-1}f(k)$ and residual $Res(g(z),p)=\frac{1}{(m-1)!}\left.\frac{\mathrm{d}^{m-1}}{\mathrm{d}z^{m-1}}\left((z-p)^mg(z)\right)\right\vert_{z=p}$ with $m$ being the multiplicity of the pole $p$ in $g$.
- Power Series: same as inverse laplace.
- Partial Fractions: same as inverse laplace.
Modified Z-Transfrom
- Definition: $F(z,m)=\mathcal{Z}_m(f,m)=\mathcal{Z}(\left\{f(kT-(1-m)T)\right\} _{k\in\mathbb{N}^+})(z)$
- We denote corresponding continuous form $\mathcal{L}(f(t-(1-m)T)\delta_ T(t))$ as $F^*(s,m)$
- Residual Theorem: $\mathcal{Z}_m(f,m)=z^{-1}\sum _{p_i} Res(\frac{F(s)e^{mTs}}{1-z^{-1}e^{Ts}}, p_i)$
- ModZ Transform is usually used when there’s delay in the system, use this transform to shift the signal with proper $m$ value.
Starred Transform
- Definition: $F^* (s)=\sum^\infty_{n=0}f(n*T)e^{-nTs}$
Starred Transform is defined in continuous s-domain, but it only aggregates on discrete s values defined periodically by sampling time T, like Z-Transform. Starred Transform is usually exchangeable with Z-Transform with $z=e^{Ts}$.
- Sometimes we also see
*as an operator to sample a continuous signal. It converts a continuous signal to discrete delta functions. (See the “Sampler” section below) - Calculation from Laplace Transform
- $F^*(s)=\sum_{p_i\in\{poles\;of\;F(\lambda)\}} Res\left(F(\lambda)\frac{1}{1-e^{-T(s-\lambda)}}, p_i\right)$
- $F^*(s)=\frac{1}{T}\sum^\infty_{n=-\infty}F(s+jn\omega_s)+\frac{e(0)}{2}$ where $\omega_s=\frac{2\pi}{T}$
- Properties:
- $F^*(s)$ is periodic in s plane with period $j\omega_s=\frac{2\pi j}{T}$
- If $F(s)$ has a pole at $s=s_0$, then $F^*(s)$ must have poles at $s=s_0+jn\omega_s$ for $m\in\mathbb{Z}$
- $A(s)=B(s)F^* (s) \Rightarrow A^* (s)=B^* (s)F^* (s)$, while usually $A(s)=B(s)F(s) \nRightarrow A^* (s)=B^* (s)F^* (s)$
Fourier Transform
Fourier transform is basically to substitute $s=j\omega$ into Laplace transform. Additional properties are not discussed here.
- One important theorem (Shannon-Nyquist Sampling Theorem): Suppose $e:\mathbb{R}_+\to\mathbb{R}$ has a Fourier Transform with no frequency components greater than $f_0$, then $e$ is uniquely determined by the signal $e_s$ generated by ideally sampling $e$ with period $\frac{1}{2}f_0$.
State Space Representation
Continuous State Space Representation
Definition
A continuous-time linear state-space system can be described by following two equations: \begin{align}&\text{State equation}:\;&\dot{x}(t)&=A(t)x(t)+B(t)u(t),&\;x(t)\in\mathbb{R}^n,\;u(t)&\in\mathbb{R}^m \\&\text{Output equation}:\;&y(t)&=C(t)x(t)+D(t)u(t),&\;y(t)&\in\mathbb{R}^p\end{align}
The input $u:[0,\infty)\to\mathbb{R}^m$, state $x:[0,\infty)\to\mathbb{R}^n$, and output $y:[0,\infty)\to\mathbb{R}^p$ are all signals, i.e. functions of continuous time $t\in[0,\infty)$. The coefficients $A\in\mathbb{R}^{n\times n}$,$B\in\mathbb{R}^{n\times m}$,$C\in\mathbb{R}^{p\times n}$,$D\in\mathbb{R}^{p\times m}$
This linear time-varying (LTV) system can be written compactly as \begin{align*} \dot{x}&=A(t)x+B(t)u \\ y&=C(t)x+D(t)u\end{align*} Similarly, linear time-invariant (LTI) system can be written as \begin{align} \dot{x}&=Ax+Bu \\ y&=Cx+Du\end{align}
For non-linear system, the equation will be written as
| time-varying (NLTV) | time-invariant (NTLI) | time-invariant autonomous |
|---|---|---|
\begin{align*}\dot{x}&=f(x,u,t)\\y&=g(x,u,t)\end{align*} | \begin{align*}\dot{x}&=f(x,u)\\y&=g(x,u)\end{align*} | \begin{align*}\dot{x}&=f(x)\\y&=g(x)\end{align*} |
Solution
Math prerequisites here:
- For definition of function on matrix, see my notes for algebra basics
- $e^A$ is matrix exponential,
expmin MATLAB
- $\frac{\mathrm{d}}{\mathrm{d}t}e^{At}=Ae^{At}=e^{At}A$
- $e^{(A+B)t}\Leftrightarrow AB=BA$ (be careful when commute matrices)
- $\mathcal{L}\{e^{At}\}=(sI-A)^{-1}$ (can be derived from property 1 and laplace derivative)
- To calculate $e^A$
- Eigenvalue decomposition
- Jordan form decomposition
- Directly evaluate infinite power series (converges quickly)
- Inverse Laplace transform
- For more properties of the matrix function, seeMatrix Algebra
For homogeneous LTI system: $$\begin{align}x(t)=e^{A(t-t_0)}x_0\end{align}$$
- “homogeneous” = zero-input, Eq.5 is also called zero input response (ZIR).
- “homogeneous equation” = 齐次方程
For LTI system: $$\begin{align}x(t)=e^{A(t-t_0)}x(t_0)+\int^t_{t_0}e^{A(t-\tau)}Bu(\tau)d\tau\end{align}$$ This result requires $A$ to be time-invariant, $B,C,D$ can be time varying.
- The solution consists of two parts: ZIR and ZSR (zero state response, $x(t_0)=0$), which are homogenenous solution (通解) and particular solution (特解) of the ODE.
- ZIR and ZSR are both linear mapping
For homogeneous LTV system: $$\begin{align}x(t)=\Phi(t,t_0)x_0\end{align}$$
- Matrix $\Phi$ is called the state transition matrix, defined as $$\begin{equation}\begin{split}\Phi(t,t_0)\equiv I+\int^t_{t_0}A(s_1)\mathrm{d}s_1+\int^t_ {t_0}A(s_1)\int^{s_1}_ {t_0}A(s_2)\mathrm{d}s_2\mathrm{d}s_1+\\ \int^t_ {t_0}A(s_1)\int^{s_1}_ {t_0}A(s_2)\int^{s_2}_ {t_0}A(s_3)\mathrm{d}s_3\mathrm{d}s_2\mathrm{d}s_1+\cdots\end{split}\end{equation}$$
- Properties of $\Phi$:
- $\Phi(t,t)=I$
- $\frac{\mathrm{d}}{\mathrm{d}t}\Phi(t,t_0)=A(t)\Phi(t,t_0)$
- (semigroup property) $\Phi(t,s)\Phi(s,\tau)=\Phi(t,\tau)$
- $\forall t,\tau\geqslant 0,\;[\Phi(t,\tau)]^{-1}=\Phi(\tau,t)$
- Eq.6 can be directly derived by evaluating Eq.8
For LTV system: $$\begin{align}x(t)=\Phi(t,t_0)x_0+\int^t_{t_0}\Phi(t,\tau)B(\tau)u(\tau)d\tau\end{align}$$
Some conclusions:
- The solution given by Eq.9 is unique
- The set of all solutions to ZIR system forms a vector space of dimension $n$
- If $A(t)A(s)=A(s)A(t)$, then $\Phi(t,t_0)=e^{\int^t_{t_0}A(\tau)\mathrm{d}\tau}$
Phase Portraits: A phase portrait is a graph of several zero-input responses on the phase plane ($\dot{x}(t)$ and $x(t)$ are phase variables)
Usually in phase portraits, there are two straight lines corresponding to the eigenvector of A, other lines are growing in or opposite to the direction of the lines.
Transfer function
- For LTI case, $\frac{Y(s)}{U(s)} = C(sI-A)^{-1}B+D$
This can be derived by take laplace transform of both sides of state equations
Discrete State Space Representation
Definition
A discrete-time linear state-space system can be described by following two equations: $$\begin{align}&\text{State eq.}:\;&x(k+1)&=A(k)x(k)+B(k)u(k),&\;x\in\mathbb{R}^n,\;u&\in\mathbb{R}^m \\ &\text{Output eq.}:\;&y(k)&=C(k)x(k)+D(k)u(k),&\;y&\in\mathbb{R}^p\end{align}$$
The input $u:\mathbb{N}\to\mathbb{R}^m$, state $x:\mathbb{N}\to\mathbb{R}^n$, and output $y:\mathbb{N}\to\mathbb{R}^p$ are all signals, i.e. functions of continuous time $t\in\mathbb{N}$.
Discrete LTI system is sometimes written compactly as $$\begin{align} x_{k+1}&=Ax_k+Bu_k \\ y_k&=Cx_k+Du_k \end{align}$$
Transfer function
- For LTI case, $H(z)=C(zI-A)^{-1}B+D$ (pulse tranfer function)
Controllability & Reachability
Note: hereafter $\mathfrak{R}$ denotes range space, $\mathfrak{N}$ denotes null space.
- Controllability: $\exists u$ that drives any initial state $x(t_0)=x_0$ to $x(t_1)=0$
- Reachability: $\exists u$ that drives initial state $x(t_0)=0$ to any $x(t_1)=x_1$
Consider the continuous LTV system $\dot{x}=A(t)x+B(t)u,\;x\in\mathbb{R}^n,u\in\mathbb{R}^m$.
Reachable Subspace: Given $t_0$ & $t_1$, the reachable subspace $\mathcal{R}[t_0, t_1]$ consists of all states $x_1$ for which there exists and input $u:[t_0, t_1]\to\mathbb{R}^m$ that transfers the state from $x(t_0)=0$ to $x(t_1)=x_1$.
- $\mathcal{R}[t_0, t_1]\equiv\left\{x_1\in\mathbb{R}^n\middle|\exists u(\cdot),\;x_1=\int^{t_1}_{t_0}\Phi(t_1,\tau)B(\tau)u(\tau)\mathrm{d}\tau\right\}$
Controllable Subspace: Given $t_0$ & $t_1$, the controllable subspace $\mathcal{C}[t_0, t_1]$ consists of all states $x_0$ for which there exists an input $u:[t_0, t_1]\to\mathbb{R}^m$ that transfers the state from $x(t_0)=x_0$ to $x(t_1)=0$
- $\mathcal{C}[t_0, t_1]\equiv\left\{x_0\in\mathbb{R}^m\middle|\exists u(\cdot),\;0=\Phi(t_1,t_0)x_0+\int^{t_1}_{t_0}\Phi(t_1,\tau)B(\tau)u(\tau)\mathrm{d}\tau\right\}$
- or $\mathcal{C}[t_0, t_1]\equiv\left\{x_0\in\mathbb{R}^m\middle|\exists u(\cdot),\;x_0=\int^{t_1}_{t_0}\Phi(t_0,\tau)B(\tau)\left[-u(\tau)\right]\mathrm{d}\tau\right\}$
Reachability Grammian: $W_\mathcal{R}(t_0, t_1)\equiv\int^{t_1}_{t_0}\Phi(t_1,\tau)B(\tau)B(\tau)^\top\Phi^\top(t_1,\tau)\mathrm{d}\tau$ given times $t_1>t_0\geqslant0$
- The system is reachable at time $t_0$ iff $\exists t_1$ s.t. $W_\mathcal{R}(t_0,t_1)$ is non-singular.
non-singular for some $t_1$ $\Rightarrow$ non-singular for any $t_1$
- $\mathcal{R}[t_0,t_1]=\mathfrak{R}(W_\mathcal{R}(t_0,t_1))$
- if $x_1=W_\mathcal{R}(t_0,t_1)\eta_1\in\mathfrak{R}(W_\mathcal{R}(t_0,t_1))$, the control $u(t)=B^\top(t)\Phi^T(t_1,t)\eta_1$,$t\in[t_0,t_1]$ can be used to transfer the system from $x(t_0)=0$ to $x(t_1)=x_1$ (w/ minimum energy)
minimum energy = minimum $\int^T_0\Vert u(\tau)\Vert^2\mathrm{d}\tau$
- For LTI system $W_\mathcal{R}(t_0,t_1)=\int^{t_1}_ {t_ 0}e^{A(t_1-\tau)}BB^\top e^{A^{\top} (t_1-\tau)}\mathrm{d}\tau=\int^{t_1-t_ 0}_ {0}e^{At}BB^\top e^{A^{\top}t}$
Controllability Grammian: $W_\mathcal{C}(t_0, t_1)\equiv\int^{t_1}_{t_0}\Phi(t_0,\tau)B(\tau)B(\tau)^\top\Phi^\top(t_0,\tau)\mathrm{d}\tau$ given times $t_1>t_0\geqslant0$
The system is reachable at time $t_0$ iff $\exists t_1$ s.t. $W_\mathcal{C}(t_0,t_1)$ is non-singular.
$\mathcal{C}[t_0,t_1]=\mathfrak{R}(W_\mathcal{C}(t_0,t_1))$
if $x_0=W_\mathcal{C}(t_0,t_1)\eta_0\in\mathfrak{R}(W_\mathcal{C}(t_0,t_1))$, control $u(t)=-B^\top(t)\Phi^\top(t_0,t)\eta_0$,$t\in[t_0,t_1]$ can be used to transfer the state from $x(t_0)=x_0$ to $x(t_1)=0$ (w/ minimum energy)
For LTI system $W_\mathcal{C}(t_0,t_1)=\int^{t_1}_ {t_ 0}e^{A(t_0-\tau)}BB^\top e^{A^{\top} (t_0-\tau)}\mathrm{d}\tau=\int^{t_1-t_ 0}_ {0}e^{-At}BB^\top e^{-A^{\top}t}$
Controllability Matrix: For LTI system, controllability matrix $\mathcal{C}=[B\;|\;AB\;|\;A^2B\;\cdots\;A^{n-1}B]$
The controllability matrix works for both continuous and discrete system, and it’s easier to be derived from discrete LTI equations: In discrete LTI, $\mathcal{C}\mathbf{u}=-A^k x_0$ where $\mathbf{u}=\begin{bmatrix}u_{k-1} & u_{k-2} & \ldots & u_0\end{bmatrix}^\top$
- For LTI, $\mathcal{R}[t_0,t_1]=\mathfrak{R}(W_\mathcal{R}[t_0,t_1])=\mathfrak{R}(\mathcal{C})=\mathfrak{R}(W_\mathcal{C}[t_0,t_1])=\mathcal{C}[t_0,t_1]$
This implies Controllability $\Leftrightarrow$ Reachability for LTI systems.
- The controllable subspace $\mathfrak{\mathcal{C}}$ is the smallest A-invariant subspace that contains $\mathfrak{\mathcal{B}}$
- If the controllability matrix has full rank, the LTI system (or the pair $(A,B)$) is completely controllable
PBH-Eigenvector Test: An LTI system is not controllable iff there exists a nonzero left eigenvector $v$ of $A$ such that $vB=0$
PBH-Rank Test: An LTI system will be controllable iff $[\lambda I-A \;| \;B]$ has full row rank for all eigenvalue $\lambda$
For LTI system, there exists an input $u(\cdot)$ that transfer the state from $x_0$ ito $x_1$ in finite time $T$ iff $x_1-e^{AT}x_0\in\mathfrak{R}(\mathcal{C})$
- The input that transfers any state $x_0$ to any other state $x_1$ in some finite time $T$ is $u(t)=B^\top e^{A^{\top}(T-t)}W_\mathcal{R}^{-1}(0,T)[x_1 -e^{AT}x_0]$, for $t\in[0,T]$ (w/ minimum energy)
Observability
Observability: Given any input $u(t)$ and output $y(t)$ over $t\in[t_0,t_1]$, it’s sufficient to determine a unique initial state $\exists !x(t_0)$.
Observability Grammian: $W_\mathcal{O}(t_0,t_1)\equiv\int^{t_1}_{t_0}\Phi^\top(t_1,\tau)C^\top(\tau)C(\tau)\Phi(t_1,\tau)\mathrm{d}\tau$
The system is observable at time $t_0$ iff $\exists t_1$ s.t. $W_{\mathcal{O}}(0,t)$ is nonsingular.
For LTI system $W_{\mathcal{O}}(t_0,t_1)=\int^{t_1}_{t_0} e^{A^{\top}(t_1-\tau)}C^\top Ce^{A(t_1-\tau)}\mathrm{d}\tau=\int^{t_1-t_0}_0 e^{A^{\top}\tau}C^\top Ce^{A\tau}\mathrm{d}\tau$
Observability Matrix: For LTI system, observability $\mathcal{O}=\begin{bmatrix}C\\CA\\CA^2\\ \vdots\\CA^{k-1}\end{bmatrix}$
The controllability matrix works for both continuous and discrete system, and it’s easier to be derived from discrete LTI equations: In discrete LTI, $\Psi_{k-1}=\mathcal{O}x_0$ where $$\Psi_k\equiv\begin{bmatrix}y_0\\y_1\\y_2\\ \vdots\\ y_{k-1}\end{bmatrix}-\begin{bmatrix} D & 0 & 0 & \cdots & 0 \\ CB & D & 0 & \cdots & 0 \\ CAB & CB & D & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ CA^{k-2}B & CA^{k-3}B & CA^{k-4}B & \cdots & 0 \end{bmatrix}\begin{bmatrix}u_0\\u_1\\u_2\\ \vdots \\ u_{k-1}\end{bmatrix}$$
- If the controllability matrix has full rank, the LTI system (or the pair $(A,C)$) is completely observable.
PBH-Rank Test: An LTI system will be observable iff $\begin{bmatrix}A-\lambda I \\C\end{bmatrix}$ has full column rank for all eigenvalue $\lambda$
Duality
- Duality Theorem: The pair $(A,B)$ is controllable iff the pair $(A^\top, B^\top)$ is observable.
- Controllability only depends on matrix $A$ and $B$ while the Observability only depends on matrix $A$ and $C$
- Duality theorem is useful for proof of observability conclusions from controllability
- Adjoint System:
| Original System | Adjoint System | |
|---|---|---|
| Equations | $$\begin{align*} \dot{x}&=A(t)x+B(t)u \\ y&=C(t)x \end{align*}$$ | $$\begin{align*} \dot{p}&=-A^*(t)p-C^*(t)v \\ z&=B^*(t)p\end{align*}$$ |
| Initial Condition | $x(t_0)=x_0$ | $p(t_1)=p_1$ |
| State Trasition Matrix | $\Phi(t,t_0)$ | $\Phi^*(t_1,t)=\left(\Phi^*(t,t_1)\right)^{-1}$ |
| Zero-State Response | $$\begin{split}L_u:\;&u(\cdot)\to x(t_1)\\=&\int^{t_1}_{t_0}\Phi(t_1,\tau)B(\tau)u(\tau)\mathrm{d}\tau\end{split}$$ | $$\begin{split}P_u:\;&v(\cdot)\to p(t_0)\\=&\int^{t_1}_{t_0}\Phi^*(\tau,t_0)C^*(\tau)v(\tau)\mathrm{d}\tau\end{split}$$ |
| Zero-Input Response | $$\begin{split}L_0:\;&x_0\to y(\cdot)\\=&C(\cdot)\Phi(\cdot,t_0)x_0\end{split}$$ | $$\begin{split}P_0:\;&p_1\to z(\cdot)\\=&B^*(\cdot)\Phi^*(t_1,\cdot)p_1\end{split}$$ |
| Duality Theorem | Controllable ($\rho(L_u)=n$) | Observable ($\rho(P_0^*)=n$) |
| Observable ($\rho(L_0^*)=n$) | Controllable ($\rho(P_u)=n$) | |
| A state is reachable ($x\in\mathfrak{R}(L_u)$) | A state is unobservable ($x\in\mathfrak{N}(L_0)$) |
Decomposition and Realizations
Similarity Transform of a (LTI) system: Based on Eq.3 and Eq.4, define $x=P\bar{x}$, then we have $$\begin{align}\dot{\bar{x}}&=P^{-1}AP\bar{x}+P^{-1}Bu&=\bar{A}\bar{x}+\bar{B}u \\ y&=CP\bar{x}+Du&=\bar{C}\bar{x}+Du\end{align}$$
- Similarity transform doesn’t affect transfer function.
Controllability Decomposition: For an uncontrollable LTI system, define matrix $V=[V_1\;V_2]$ where $V_1$ is a basis for $\mathfrak{R}(\mathcal{C})$ and $V_2$ complete a basis for $\mathbb{R}^n$, then after similarity transform with $\bar{x}=V^{-1}x$, we can partition the system like following: $$\begin{align*}\dot{\bar{x}}&=\bar{A}\bar{x}+\bar{B}u&=&\begin{bmatrix}\bar{A}_ {11}&\bar{A}_ {12} \\ \mathbf{0} & \bar{A} _{22}\end{bmatrix}\begin{bmatrix}\bar{x} _1 \\ \bar{x} _2\end{bmatrix}+\begin{bmatrix}\bar{B} _1 \\ \mathbf{0}\end{bmatrix}u \\ y&=\bar{C}\bar{x}+Du&=& \begin{bmatrix}\bar{C} _1 & \bar{C} _2\end{bmatrix}\begin{bmatrix}\bar{x} _1 \\ \bar{x} _2\end{bmatrix} + Du\end{align*}$$ Here $\bar{x}_2$ is uncontrollable, and ZSR of the system with or without $\bar{x}_2$ is the same.
Observability Decomposition: For an unobservable LTI system, define matrix $U=\begin{bmatrix}U_1\\U_2\end{bmatrix}$ where $U_1$ is a basis for $\mathfrak{R}(\mathcal{O}^\top)$ and $U_2$ complete a basis for $\mathbb{R}^n$, then after similarity transform with $\hat{x}=Ux$, we can partition the system like following: $$\begin{align*}\dot{\hat{x}}&=\hat{A}\hat{x}+\hat{B}u&=&\begin{bmatrix}\hat{A}_ {11}&\mathbf{0} \\ \hat{A}_ {21} & \hat{A} _{22}\end{bmatrix}\begin{bmatrix}\hat{x} _1 \\ \hat{x} _2\end{bmatrix}+\begin{bmatrix}\hat{B} _1 \\ \hat{B} _2\end{bmatrix}u \\ y&=\hat{C}\hat{x}+Du&=& \begin{bmatrix}\hat{C} _1 & \mathbf{0}\end{bmatrix}\begin{bmatrix}\hat{x} _1 \\ \hat{x} _2\end{bmatrix} + Du\end{align*}$$
Realization: $\Sigma$ (system with Eq.3 and Eq.4) is a realization of $H(s)$ iff $H(s)=C(sI-A)^{-1}B+D$.
- Equivalent: Two realizations are said to be equivalent if they have the same transfer function
- Algebraically Equivalent: Two realizations have same transfer function and $n$ (dimension of states). (this implies a similarity transform between them)
- Minimal Realization: $\Sigma$ is a minimal realization of $H(s)$ iff there doesn’t exists an equivalent realization $\bar{\Sigma}$ with $\bar{n}< n$
$\Sigma$ is a minial realization iff $\Sigma$ is completely controllable and observable.
Kalman Cannonical Structure Theorem (aka. Kalman Decomposition): suppose $\rho(\mathcal{C})< n$ and $\rho(\mathcal{O})< n$, $\mathfrak{R}(\mathcal{C})$ are the controllable states, $\mathfrak{N}(\mathcal{O})$ are the unobservable states, define subspaces:
| Subspaces | Controllable | Observable |
|---|---|---|
| $V_2\equiv\mathfrak{R}(\mathcal{C})\cup\mathfrak{N}(\mathcal{O})$ | Yes | No |
| $V_1$ s.t. $V_1\oplus V_2=\mathfrak{R}(\mathcal{C})$ | Yes | Yes |
| $V_4$ s.t. $V_4\oplus V_2=\mathfrak{N}(\mathcal{O})$ | No | No |
| $V_3$ s.t. $V_1\oplus V_2\oplus V_3\oplus V_4=\mathbb{C}^n$ | No | Yes |
| Then let $$\begin{align*}\tilde{x}=\begin{bmatrix}\tilde{x}_ 1\\ \tilde{x}_ 2\\ \tilde{x}_ 3\\ \tilde{x}_ 4\end{bmatrix},\;\tilde{A}=&\begin{bmatrix}A_ {\mathrm{co}} &&A_{13}&\\A_{21}&A_{\mathrm{c\bar{o}}}&A_{23}&A_{24}\\&&A_{\mathrm{\bar{c}o}}&\\&&A_{43}&A_{\mathrm{\bar{c}\bar{o}}} \end{bmatrix},\;\tilde{B}=\begin{bmatrix}B_{\mathrm{co}}\\ B_{\mathrm{c\bar{o}}} \\ \mathbf{0} \\ \mathbf{0} \end{bmatrix} \\ \tilde{C}=&\begin{bmatrix}C_{\mathrm{co}}&\mathbf{0}\quad&C_{\mathrm{\bar{c}o}}&\mathbf{0}\quad\end{bmatrix}\end{align*}$$ | ||
| $$\tilde{\Sigma}:\begin{cases} \dot{\tilde{x}}=A_{\mathrm{co}}\tilde{x}_ 1+B_{\mathrm{co}}u_1\\ y=C_{\mathrm{co}}\tilde{x}_1\end{cases}$$ |
$\tilde{\Sigma}$ is completely controllable and completely observable.
Consider SISO systems $$H(s)=\frac{b(s)}{a(s)}=\frac{b_{n-1}s^{n-1}+\ldots+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+\ldots+a_1s+a_0}=\frac{\sum^{n-1}_{j=0} b_js^j}{s^n+\sum^{n-1}_{i=0} a_is^i}=\frac{Y(s)}{U(s)}$$
- Controllable Cannonical Form: $$\begin{align}\dot{x}&=\begin{bmatrix} 0&1&&\\ \vdots & & \ddots & \\ 0&&&1 \\-a_0&-a_1&\cdots&-a_{n-1}\end{bmatrix}x+\begin{bmatrix}0\\ \vdots \\ 0 \\ 1\end{bmatrix}u&=&A_cx+B_cu\\ y&=\begin{bmatrix}\quad b_0 &\quad b_1 &\cdots & \quad b_{n-1}\end{bmatrix}x&=&C_cx \end{align}$$
- $(A_c, B_c)$ is controllable
- $(A_c, C_c)$ is observable if $a(s)$ and $b(s)$ have no common factors
- Observable Cannonical Form: $$\begin{align}\dot{x}&=\begin{bmatrix} 0&&&&-a_0\\ 1 & \ddots &&&-a_1 & \\ &\ddots&\ddots&&\vdots \\&&\ddots&0&-a_{n-2} \\ &&&1&-a_{n-1}\end{bmatrix}x+\begin{bmatrix}b_0\\ b_1 \\ \vdots \\ b_{n-2} \\ b_{n-1}\end{bmatrix}u&=&A_ox+B_ou\\ y&=\begin{bmatrix}0 & \;\cdots &\;\cdots & 0 & \quad 1\qquad \end{bmatrix}x&=&C_ox \end{align}$$
- $(A_o, C_o)$ is observable
- $(A_o, B_o)$ is controllable if $a(s)$ and $b(s)$ have no common factors
- Model Cannonical Forms: Do Spectral Decomposition (eigen-decomposition) or Jordan Decomposition, and then use the modal matrix (matrix of eigenvectors) to do similarity transform.
- The Gilbert Realization: Let $G(s)$ be a $p\times m$ rational transfer function with simple poles (nonrepeated) at $\lambda_i,\;i=1,2,\ldots,k$. Calculate partial fraction expansion $$G(s)=\sum^k_{i=1}\frac{R_i}{s-\lambda_i},\qquad \text{Residue}\;R_i=\lim_{s\to\lambda_i}(s-\lambda_i)G(s)$$ Let $r_i=\rho(R_i)$, now write $R_i=C_iB_i$ where $C_ i\in\mathbb{R}^ {p\times r_ i},\;B_ i\in\mathbb{R}^ {r_ i\times p}$, then write $$A=\mathrm{blkdiag}\{\lambda_i I_{r_i}\},\;B^\top=[B_1^\top \;\cdots\; B^\top_k],\;C=[C_1\; \cdots\;C_k]$$, then $(A,B,C)$ is a realization of $G(s)$ with order $n=\sum^k_1 r_i$
For MIMO system the cannonical forms with be quite complex:
- Controllable Cannonical Form (for MIMO): Here we provide a way to convert from controllable LTI system to controllable. The collection of independent columns of $\mathcal{C}$ may be expressed as $$M=[b_1\;Ab_1\; \cdots\;A^{\mu_1-1}b_1\;|\;b_2\;Ab_2\;\cdots\;A^{\mu_2-1}b_2\;|\;\cdots\;|\;b_p\;Ab_p\;\cdots\;A^{\mu_p-1}b_p]$$ Construct $M^{-1}$ and then $T$:$$M^{-1}=\left[m_{11}^\top\;m_{12}^\top\;\cdots\;m_{1\mu_1}^\top\;\middle|\;\cdots\;\middle|\;m_{p1}^\top\;m_{p2}^\top\;\cdots\;m_{p\mu_p}^\top \right]^\top$$ $$T=\left[m_{1\mu_1}^\top\;(m_{1\mu_1}A)^\top\;\cdots\;\left(m_{1\mu_1}A^{\mu_1-1}\right)^\top\;\middle|\;\cdots\;\middle|\; m_{p\mu_p}^\top\;(m_{p\mu_p}A)^\top\;\cdots\;\left(m_{p\mu_p}A^{\mu_p-1}\right)^\top\right]^\top$$ Perform similarity transform with $\bar{x}=Tx$ and the canonical form will be obtained like following: $$\bar{A}=\begin{bmatrix}\bar{A}_ {\mu_1\times\mu_1}&\mathbf{0}_ {\cdot\cdot}&\cdots&\mathbf{0}_ {\cdot\cdot} \\ \mathbf{0}_ {\cdot\cdot}&\bar{A}_ {\mu_2\times\mu_2}&\cdots&\mathbf{0}_ {\cdot\cdot}\\ \vdots&\vdots&\ddots&\vdots \\ \mathbf{0}_ {\cdot\cdot}&\mathbf{0}_ {\cdot\cdot}&\cdots&\bar{A}_ {\mu_ p\times\mu_ p} \end{bmatrix},\quad\bar{B}=\begin{bmatrix}\mathbf{0}_ {\cdot n}\\ \mathbf{0}_ {\cdot (n-1)}\\ \vdots\\ \mathbf{0}_ {\cdot 1}\end{bmatrix}$$ Here $\bar{A}_ {\mu_ i\times\mu_ i}$ is the same structure as in SISO, $\mathbf{0}_ {\cdot\cdot}$ is a zero matrix except the last row, $\mathbf{0}_ {\cdot i}$ is a zero matrix except for the last row, and in the last row there are $i$ non-zeros on the right with the first element being 1.
System Performance
System Characteristic Equation: The polynomical with the roots equal to the poles of the output that are independent of the input.
System Type: A plant $G$ can always be written as $G(s)=\frac{K\prod^m_{i=1}(s-s_i)}{s^N\prod^p_{j=1}(s-s_j)},\;z_i,z_j\neq 0$ or $G(z)=\frac{K\prod^m_{i=1}(z-z_i)}{(z-1)^N\prod^p_{j=1}(z-z_j)},\;z_i,z_j\neq 1$. Here $N$ is called the system type of $G(z)$.
Properties that matters for a controller:
- Stability
- Steady state accuracy
- Transient response
- Sensitivity
- Exogenous disturbance rejection
- Bounded control effort
Stability
- Stability means when the time goes to infinity, the system response is bounded.
- A system is stable if all its poles lies in the left half of $s$-plane or all inside the unit circle of $z$-plane.
- A system is marginally stable if one of the pole is on the imaginary axis of $s$-plane or on the unit circle of $z$-plane.
- Stability of linear systems is independent of input
- The stability of a linear system can be evaluated by its characteristic equation $1-G_{op}(z)=0$, where $G_{op}$ is the open-loop transfer function (transfer function when input is eliminated, or feedback route is cut off).
- Methods to evaluate stability
- Routh-Hurwitz Criterion: $s$-plane (omited here, see Wikipedia)
- For discrete system, a strategy is use bilinear transformation: $z=e^{\omega T}\approx \frac{1+\omega T/2}{1-\omega T/2}$
- Jury Criterion: $z$-plane (see Wikipedia)
- Root Locus Method: both $s$- and $z$-plane (see Wikipedia,
rlocusin MATLAB) - Nyquist Criterion: both $s$- and $z$-plane (see Wikipedia,
nyquistin MATLAB)- It works for both continuous and discrete systems, the difference is that in $s$-plane the detour point is at $s=0$ while in $z$-plane the detour point is at $z=1$.
- Bode Diagrams: draw frequency response for (pulse) transfer function, works for both $s$- and $z$-plane (see Wikipedia,
bodein MATLAB)
A review of the stability judgement method here at 知乎
- Routh-Hurwitz Criterion: $s$-plane (omited here, see Wikipedia)
Lyaponov Stability
Lyaponove Stability is only concerned with the effect of initial conditions on the response of the system (ZIR)
- Equilibrium Point $x_e$: Consider NLTV $\dot{x}(t)=f(x(t),u(t),t)$, equilibrium point satisfies $x(t_0)=x_e,\;u(t)\equiv 0\Rightarrow x(t)=x_e,\;\text{i.e. }f(x_e,0,t)=0,\;\forall t>t_0$
- For discrete system, it’s $x(k+1)=x(k)=x_e$
- For LTI system, $x_e$ can be calculated from $Ax_e=0$, so the origin $x=0$ is always an equilibrium point.
- Set of equilibrium points in LTI systems are connected.
- Lyapunov stability: An equilibrium point $x_e$ of the system $\dot{x}=A(t)x$ is stable (in the sense of Lyapunov) iff $\forall \epsilon>0,\;\exists \delta(t_0,\epsilon)>0$ s.t. $\Vert x(t_0)-x_e\Vert<\delta\Rightarrow\Vert x(t)-x_e\Vert <\epsilon,\;\forall t>t_0$
- $x_e$ is uniformly stable if $\delta=\delta(\epsilon)$ (regardless of $t_0$)
- $x_e$ in LTI is stable $\Rightarrow x_e$ is uniformly stable
- $x_e$ is asymptotically stable if $\Vert x(t)-x_e\Vert\to 0$ as $t\to 0$
- $x_e$ is exponentially stable if $\Vert x(t)-x_e\Vert \leqslant \gamma e^{-\lambda(t-t_0)}\Vert x(t_0)-x(e)\Vert$
- $x_e$ in LTI is asymptotically stable $\Rightarrow x_e$ is exponentially stable
- $x_e$ is globally stable if $\delta$ can be chosen arbitrarily large
- For LTV system, the system is stable (the zero solution is stable) iff $\Phi(t,t_0)$ is bounded by $K(t_0)$.
- If bounded by constant $K$, then the system is uniformly stable.
- If bounded by constant $K$ and $\Vert\Phi(t,0)\Vert\to 0$ as $t\to 0$, then the system is asymptotically stable.
- For LTI system $\dot{x}=Ax$, it is Lyapunov stable iff $\mathrm{Re}(\lambda_i)\leqslant 0$ or $\mathrm{Re}(\lambda_i)=0,\;\eta_i=1$. ($\eta_i$ is the multiplicity of $\lambda_i$)
- If $\mathrm{Re}(\lambda_i)<0$, then the system is asymptotically stable
- Internal stability: concerns the state variables
- External stability: concerns the output variables
Notes for contents below:
- Positive definite (pd.) function: function $V$ is pd. wrt. $p$ if $V(x)>0,\;x\neq p$ and $V(x)=0,\;x=p$
- $C^n$ denotes the set of continuous and at least n-th differentiable functions
Lyapunov’s Direct Method: Let $\mathcal{U}$ be an open neighborhood of $p$ and let $V:\mathcal{U}->\mathbb{R}$ be a countinuous positive definite $C^1$ function wrt. $p$, we have following two conclusions:
- If $\dot{V}\leqslant 0$ on $\mathcal{U}\backslash\{p\}$ then $p$ is a stable fixed point of $\dot{x}=f(x)$
- If $\dot{V}< 0$ on $\mathcal{U}\backslash\{p\}$ then $p$ is an asymptotically stable fixed point of $\dot{x}=f(x)$
Lyapunov Function:
- A function satisfying conclusion 1 is called a Lyapunov function
- A function satisfying conclusion 2 is called a strict Lyapunov function
- A function that is $C^1$ and pd. is called a Lyapunov function candidate
The energy function usually can be used as Lyapunov function. If it’s only semi-positive definite, one can use LaSalle’s Theorem
For LTI system, the zero solution of $\dot{x}=Ax$ is asymptotically stable iff $\forall$ pd. hermitian matrices $Q$, equation $A^*P+PA=-Q$ has a unique hermitian solution $P$ that is positive definite.
- $A^*P+PA=-Q$ is called Lyapunov’s Matrix Equation
here $V(x)=x^* Px=\int^\infty_0 x^*(t)Qx(t)dt$, which can be also called cost-to-go, or generalized energy
Lyapunov’s Indirect Method (Lyapunov’s First Method / Lyapunov’s Linearization Theorem): The nonlinear system $\dot{x}=f(x)$ is (locally) asymptotically stable near the equilibrium point $x_e$ if the linearized system $\dot{x}_L=\frac{\partial f}{\partial x}(x_e)x_L$ is asymptotically stable.
Bounded-Input Bounded-Output Stability
BIBO stability is only concerned with the response of the system to the input (ZSR).
- Bounded-Input Bounded-Output (BIBO) stability: The LTV system is said to be (uniformly) BIBO stable if there exists a finite constant $g$ s.t. $\forall u(\cdot)$, its forced response $y_f(\cdot)$ satisfies $$ \sup_{t\in[0,\infty)}\Vert y_f(t)\Vert \leqslant g \sup_{t\in[0,\infty)} \Vert u(t)\Vert $$
The impulse response can be analyzed to assess BIBO stability The LTV system is uniformly BIBO stable iff every entry of $D(t)$ is bounded and $\sup_{t\geqslant 0}\int^t_0|g_{ij}(t,\tau)|d\tau <\infty$ for every entry $g_{ij}$ of the matrix $C(t)\Phi(t,\tau)B(\tau)$.
- BIBO stability is related with the stability descibed in classical control theory.
- Exponential Lyapunov Stability $\Rightarrow$ BIBO stability
Steady State Accuracy
Steady state accurary can be derived from the property of Laplace/Z-transform as mentioned above (assuming stability) $$\lim\limits_{t\to \infty} f(t) = \lim\limits_{z\to 1} (z-1)F(z) = \lim\limits_{s\to 0}sF(s)$$
Transient Response
Some measurements of transient response (with step input):
- Rise time $t_r$: time from 10% to 90% of steady state value
- Peak overshoot: $M_p$ for overshoot magnitude and $t_p$ for time
- Settling time $t_s$: time after which the magnitude fall in $1-d$ to $1-d$ final value. $d$ is usually %2~5.
Sensitivity
Given a transfer function $H(z)$ with parameter $\Theta\in\mathbb{R}$, then sensitivity is defined as $S_H=\frac{\partial H}{\partial \Theta}\cdot\frac{\Theta}{H} = \frac{\partial H/H}{\partial \Theta/\Theta}$
Discretization and Linearization
Discretization Example
The following image shows a minial example of sampling and hold.
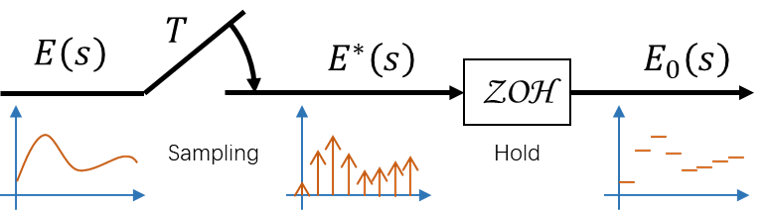
Sampling (A/D)
- Ideal sampler (a.k.a impulse modulator) converts a continuous signal $e: \mathbb{R}_+ \to \mathbb{R}$ to a discrete one $\hat{e}: \mathbb{N}\to \mathbb{R}$, such that $$ \hat{e}=e(t)\delta(t-kT)=e(t)\delta_T(t); \forall k\in \mathbb{N} $$
- Ideal sampler is actually applying starred transform.
- How to sample? A rule of thumb used to select sampling rates is chosing a rate of at least 5 samples per time constant.
- The $\tau$ appearing in the transient response term $ke^{-t/\tau}$ of a first order analog system is called the time constant.
- If the sampling time is too large, it can make the system unstable.
Reconstruction/Hold (D/A)
- Zero order hold (ZOH): $ZOH(\{e(k)\}_{k\in\mathbb{N}})(t) = e(k)\;for\;kT\leq t\leq (k+1)T$
- Alternative form: $ZOH(\{e(k)\})=\sum^\infty_{k=0}e(k)(H(t-kT)-H(t-(k+1)T))$
- Its Laplace Transform: $G_{ZOH}(s)=\frac{1-e^{-Ts}}{s}$
- First order hold (FOH): (delayed version) $$FOH(\{e(k)\}_ {k\in\mathbb{N}})(t)=\sum_ {k\in\mathbb{N}}\left[e(kT)+\frac{t-kT}{T}(e(kT)-e((k-1)T)) \right]\left[H(t-kT)-H(t-(k+1)T) \right]$$
State Space Representation
Suppose we are given the LTI continuous system $$\begin{align*} \dot{x}(t) &= Ax(t)+Bu(t) \\ y(t)&=Cx(t)+Du(t) \end{align*}$$ If the input is sampled and ZOH and the output is sampled, then $$\begin{align*} x(k+1)&=\bar{A}x(k)+\bar{B}u(k) \\ y(k)&=\bar{C}x(k)+\bar{D}u(k)\end{align*}$$ where $\bar{A}=\Phi((k+1)T,kT)=e^{AkT}$$\bar{B}=\int^{(k+1)T}_{kT}\Phi((k+1)T,\tau)B\mathrm{d}\tau=A^{-1}(e^{AT}-I)$$\bar{C}=C$ and $\bar{D}=D$
Steps to apply conversion:
- Dervice SS model for analog system
- Calculate discrete representation (
c2din MATLAB)- Calculate pulse transfer function (
ss2tfin MATLAB) If there is a complex system with multiple sampling and holding, a general rule is
- Each ZOH output is assumed to be an input
- Each sampler input is assumed to be an output and then create continuous state space from analog part of the system, then discretize them to generate discrete equations
$s$-plane and $z$-plane
When converting $s$ to $z$, the complex variables are related by $z=e^{Ts}$. Suppose $s=\sigma+j\omega$, then $z=e^{T\sigma}\angle \omega T$
Note: if frequencies differ in integer multiples of the sampling frequency $\frac{2\pi}{T}=\omega_s$, then they are sampled into the same location in the $z$-plane.
For transient response relationship, suppose $s$-plane poles occur at $s=\sigma\pm j\omega$, then the transient response if $Ae^{\sigma t}\cos(\omega t+\varphi)$. When sampling occurs at $z$-plane poles, then the transient response if $Ae^{\sigma kT}\cos(\omega kT+\varphi)$.
Example: 2nd order transfer function
$$G(s)=\frac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2}$$ The $z$-plane poles occur at $z=r\angle\pm\theta$ where $r=e^{-\xi\omega_n T}$ and $\theta=\omega_n T\sqrt{1-\xi^2}$.Then we can get the inverse relationship
- $\xi=-\ln( r)/\sqrt{\ln^2( r)+\theta^2}$
- $\omega_n=(1/T)\sqrt{\ln^2( r)+\theta^2}$
- (time constant) $\tau=-T/\ln( r)$
Linearization
- Jacobian Linearization: linearize $\dot{x}=f(x,u)$ at an equilibrium $(x_e, u_e)$ is $$\frac{\mathrm{d}z}{\mathrm{d}t}=Az+Bv,\quad\text{where}\;A=\left.\frac{\mathrm{d}f}{\mathrm{d}x}\right|_ {\begin{split}x=x_e\\u=u_e\end{split}},\;B=\left.\frac{\mathrm{d}f}{\mathrm{d}u}\right|_ {\begin{split}x=x_e\\u=u_e\end{split}},\;z=(x-x_e),\;v=(u-u_e)$$
- change $(x_e, u_e)$ to a trajectory $(x_e(t), u_e(t))$ we can linearize the system about a trajectory.
Controllers
Full State Feedback
This method can be used for both continuous and discrete systems, just make sure to use corresponding method for choosing correct closed-loop transfer function.
For state space systems, with access to all of the state variables, we can change the $A$ matrix and thereby change the system dynamics by feedback.
Consider SISO LTI system ($u\in\mathbb{R},y\in\mathbb{R}$), we define the input as $u\equiv Kx+Ev$ where $K\in\mathbb{R}^{1\times n},\;E\in\mathbb{R}$ is an input matrix and $v(t)\in\mathbb{R}^\mathbb{R}$ is the exogeneous (externally applied) input. The new system will be $$\begin{align}\dot{x}&=(A+BK)x+BEv\\y&=(C+DK)x+DEv\end{align}$$ The mission is to find a state update matrix $A_{\mathrm{CL}}\equiv A+BK$ with desired set of eigenvalues, therefore we can construct $A_{\mathrm{CL}}$ with specific eigenvalues and then calculate $K$. This process will be quite easy if the system is already in controllable cannonical form. (which can be constructed directly from transfer function or using similarity transform)
Another way (SISO only) to calculate $K$ without controllable cannonical form is using the following formulae given the desired characteristic polynomial $\phi^{\star}(s)=s^n+\sum^{n-1}_ {i=0} a^\star_i s^i$ and original characteristic polynomial $\phi(s)=s^n+\sum^{n-1}_ {i=0} a_i s^i$
- Ackermann’s Formula: $K=-e^\top_n\mathcal{C}^{-1}\phi^\star(A)$ (here $e_i$ is unit vector with 1 at i-th position)
- Bass-Gura’s Formula: $$K=-[(a^\star_{n-1}-a_{n-1}) \;\cdots\;(a^\star_0-a_0)]\begin{bmatrix}1&a_{n-1}&a_{n-2}&\cdots&a_1\\&1&a_{n-1}&\cdots&a_2\\ &&\ddots&\ddots&\vdots \\ &&&1&a_{n-1}\\ &&&&1\end{bmatrix}^{-1}\mathcal{C}^{-1}$$
Note that the zeros of transfer function will not be affected by state feedback.
State Estimation (Observer Design)
Some times we don’t have the direct access to the state, we need construct an observer. For stochastic version, please check my notes for stochastic system.
Assume a plant $\Sigma$ and an (Luenberger) observer $\hat{\Sigma}$: $$\Sigma:\begin{cases}\dot{x}=Ax+Bu\\ y=Cx\end{cases},\quad \hat{\Sigma}:\begin{cases} \dot{\hat{x}}=A\hat{x}+Bu+L(y-\hat{y})\\ y=C\hat{x}\end{cases}$$
Subtract observer dynamics from plant dynamics and define $e\equiv x-\hat{x}$, the dynamics for $e$ is $\dot{e}=(A-LC)e$ and $y-\hat{y}=Ce$. This error dynamic $A_e=A-LC$ can be easily changed with observable cannonical form. (which similarly can be constructed directly from transfer function or using similarity transform)
- Reduced-order Observer: If the state length of the system $n$ is large while $n-p$ is small, split the system and let $x_1$ holds the states that can be measured directly while $x_2$ holds states that are to be estimated, (i.e. $y=x_1+Du$). Define $z=\hat{x}_2-Lx_1$ then the system runs like $$\begin{align*}\begin{bmatrix}x_1 \\ \hat{x}_2\end{bmatrix}&=\begin{bmatrix} y-Du\\ z+Lx_1 \end{bmatrix}\qquad\begin{split}&\text{measurement} \\ &\text{observer}\end{split} \\ u&=K\begin{bmatrix}x_1 \\ \hat{x}_2 \end{bmatrix} + v \qquad\text{control law}\end{align*}$$ And then the error we care about is only $e=x_2-\hat{x}_2$.
- Ackermann’s Formula: $L=\phi^\star(A)\mathcal{O}^{-1}e_n$ ($\phi^\star$ is the desired characteristic function for $A_e$)
- Separation Principle: If a stable observer and stable state feedback are designed for an LTI system, then the combined observer and feedback will be stable.
Errors from state estimation
- Inaccurate knowledge of $A$ and $B$
- Initial condition uncertainty
- Disturbance or sensor error It’s advised to choose observer poles to be 2-4x faster than closed loop poles
LQR
Motivation: handle control constraints and time varying dynamics with performance metric (ideas of optimal control) Note: $x^\top Ax$ is called a quadratic form, $x^\top Ay$ is called a bilinear form
- A quadratic function $f(x)=x^\top Dx+C^\top x+c_0$ has one minimizer iff $D\succ 0$, or multiple minimizers iff $D\succeq 0$.
- (discrete finite time) Linear Quadratic Regulator (LQR): the control problem is defined as $$\begin{align*}\min_{u\in\left(\mathbb{R}^m\right)^{\{0,\ldots,N\}}} J_{N}(u,x_0)&=\frac{1}{2}\sum^{N}_{k=0}(x^\top(k)Q(k)x(k)+u^\top(k)R(k)u(k)) \\ \mathrm{s.t.}\qquad x(k+1) &= A(k)x(k) + B(k)u(k)\quad \forall k\in\{0,\ldots,N-1\}\\ y(k)&=C(k)x(k)\\ x(0)&=x_0\end{align*}$$ where $Q(k)\succ 0$ and $R(k)\succ 0$
- Bellman’s Principle of Optimality: If a closed loop control $u^\star$ is optimal over the interval $0\leqslant k\leqslant N$, it’s also optimal over any subinterval $m\leqslant k\leqslant N$ where $m\in\{0,\ldots,N\}$
- The Minimum Principle: The optimal input to the LQR problem satisfies the following backward equations: $$\begin{align*}u^\star(k)&=-K(x)x(k) \\ K(k)&=\left[B^\top(k) P(k+1)B(k)+\frac{1}{2}R(k)\right]^{-1}B^\top(k)P(k+1)A(k) \\ P(k)&=A^\top(k)P(k+1)[A(k)- B(k)K(k)]+\frac{1}{2}Q(k)\end{align*}$$ and $P(N)=Q(N),\;K(N)=0$. The optimal cost is $J^\star_N=x^\top(0)P(0)x(0)$
- For infinite horizon, $K(k)$ start becoming constants. The optimal input for LQR problem (assuming the system became LTI when $N\to\infty$) is $u^*(k)=-Kx(k)$ where $$K=(B^\top PB+R/2)^{-1}B^\top PA$$ and $P\succ 0$ is the unique solution to the discrete-time algebraic Riccati Equation: $$P=A^\top PA-A^\top PB\left(B^\top PB+R/2\right)^{-1}B^\top PA+Q/2$$